Using jugs of known capacities to get certain quantity

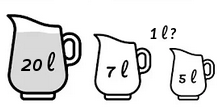
Suppose you only have a few containers of known capacities for measuring quantities, for example two jugs of 5 and 7 litres of capacity respectively, and you want to use them to obtain exactly 1 litre, for example. Can you do it?

To solve this kind of problems, I wrote a simple Perl program, jugs.pl, that explores the solutions using a brute-force backtracking algorithm limiting its recursivity level for finding the solutions with minimum steps.

There are two versions of these problems, one having a limited quantity of the substance to be moved from one jug to another, and other having an unlimited quantity available to fill any jug and discard it. My program only supports the first version, since the second one can be simulated by creating one jug filled with a large quantity that represents the source and sink of the substance, for example:

This way you can use the program to print a solution for the problem:

$ perl jugs.pl 20,7,5 20,0,0 1
(12) (7) (1)    1->3 3->2 1->3 3->2 2->1 3->2 1->3 3->2
$ perl jugs.pl
Use: perl jugs.pl M1,M2,...,MX I1,I2,...,IX N [NUMSTEPS]
Minimum steps to obtain N units in one of X jugs
given the Maximum and Initial quantity for each jug.

This way you can explore different configurations to learn more from the problem, even setting the number of steps of the solutions. Enjoy!